Zillow 是美国最大的房地产信息市场之一,也是机器学习 (ML) 这一极具影响力技术的应用典范。Zillow Research 使用 ML 模型来分析每处房产的数百个相关数据点,从而估算房屋价值并预测市场行情变化。本章介绍如何使用 Apache Spark ML 随机森林回归算法来预测某地区房屋的销售价格中值。请注意,目前 Spark ML 中只有 XGBoost 经过 GPU 加速,我们会在下一章介绍这一点。
使用 Apache Spark 机器学习预测房价
分类和回归
分类和回归是监督式机器学习算法的两个类别。监督式 ML 也称为预测分析,可利用算法来找出加标签数据中的模式,然后使用可识别这些模式的模型来预测新数据的标签。分类和回归算法采用带标签(也称为目标结果)和特征(也称为属性)的数据集,并学习如何基于这些数据特征标记新数据。

分类可识别某个项目所属的类别,如信用卡交易是否合法。回归可预测连续数值,例如房价。
回归
回归可估计目标结果因变量(标签)与一个或多个自变量(特征)之间的关系。回归可用于分析标签和特征变量之间的关系强度,通过调整一个或多个特征变量来确定标签的变化量,并预测标签和特征变量之间的趋势。
我们来看一下有关房价的线性回归示例,其中给定了历史房价以及房屋面积(以平方英尺计)、卧室数量和位置等房屋特征:
- 我们要预测什么呢?
我们的预测对象即为标签:房价 - 可利用哪些数据属性来预测?
可利用以下特征:要构建回归模型,您可以提取与标签关系最密切且对预测最有帮助的重要特征。
在以下示例中,我们将使用房屋面积作为数据特征。

线性回归对 Y“标签”与 X“特征”之间的关系进行建模,, in this case the relationship between the house price and size, with the equation: Y = 截距 +(系数 * X)+ 误差。系数用于衡量特征对标签的影响,本例中即房屋面积对房价的影响。

多重线性回归可对两个或更多“特征”和一个“标签”之间的关系进行建模。例如,若要对房价与房屋面积、卧室数量和卫生间数量之间的关系进行建模,多重线性回归函数将如下所示:
Yi = β0 + β1X1 + β2X2 + · · · + βp Xp + Ɛ
Price = = 截距 +(系数 1 * 面积)+(系数 2 * 卧室数量)+(系数 3 * 卫生间数量)+ 误差。
系数用于衡量每个特征对房价的影响。
决策树
决策树将创建一个模型,该模型通过评估一组遵循 if-then-else 模式的规则来预测标签。if-then-else 特征问题为节点,答案“true”或“false”则为决策树中指向子节点的分支。
决策树模型会估算在评估做出正确决策的概率时所需的最少 true/false 问题数。 决策树可用于分类以预测类别或某类别的概率,或用于回归以预测连续数值。以下示例展示了通过简化版决策树预测房价的具体流程:
- 问题 1:如果房屋面积 > 2000 平方英尺
- T:问题 2:如果卧室数量 > 3
- T:问题 3:如果卫生间数量 > 3
- T: Price=$400,000
- F: Price=$200,000
- T:问题 3:如果卫生间数量 > 3
- T:问题 2:如果卧室数量 > 3

随机森林
集成学习算法结合了多种机器学习算法,可获得更出色的模型。随机森林是用于分类和回归的一种主流集成学习方法。该算法基于训练阶段中不同的数据子集,构建出由多个决策树组成的模型。然后结合所有树的输出来作出预测,以便缩小方差并提高预测准确性。 使用随机森林分类会将标签预测为大多数决策树所预测的类。而使用随机森林回归时,标签为各个决策树的回归预测均值。

Spark 提供了以下回归算法:
- 线性回归
- 广义线性回归
- 决策树回归
- 随机森林回归
- 梯度提升树回归
- XGBoost 回归
- 生存回归
- 保序回归
机器学习工作流程
机器学习是一个迭代过程,其中包括:
- 提取、转换和加载 (ETL) 历史数据并对此类数据进行分析,从而提取出重要特征和标签。
- 训练、测试和评估 ML 算法的结果,以构建模型。
- 将模型用于生产过程,并使用新数据作出预测。
- 使用新数据监控和更新模型。
使用 Spark ML 流程
必须将 ML 算法要使用的特征和标签置入某个特征向量中,该向量为数字向量,代表每个特征的值。特征向量用于训练、测试和评估 ML 算法的结果,以构建最佳模型。

参考学习 Spark
Spark ML 提供了一套统一的高级别 API,这些 API 基于 DataFrame 构建,用于搭建 ML 流程或 ML 工作流程。基于 DataFrame 构建 ML 流程可实现分区数据处理的可扩展性,且便于通过 SQL 操作数据。

在 Spark ML 流程中,我们通过转换器传递数据并提取特征,使用估测器生成模型,并使用评估器测量模型的准确性。
- 转换器:转换器是将一种 DataFrame 转换为另一种 DataFrame 的算法。我们将使用转换器来创建带特征向量列的 DataFrame。
- 估测器:估测器是可对 DataFrame 进行拟合以生成转换器的算法。我们将使用估测器来训练模型,然后返回转换器模型,以便将预测列添加到带特征向量列的 DataFrame 中。
- 流程:流程将多个转换器和估测器相连接,从而指定 ML 工作流程。
- 评估器:评估器根据标签和 DataFrame 预测列评估所训练模型的准确性。
用例数据集示例
在本示例中,我们将使用由 StatLib 库提供的加利福尼亚房价数据集。该数据集包含基于 1990 年加利福尼亚人口普查数据的 20640 条记录,每条记录均代表一个地理街区。以下列表给出了有关数据集属性的说明。
- 房价中值:街区内各家房屋的房价中值(以千美元计)。
- 经度:东西向测量值,越往西数值越大。
- 纬度:南北向测量值,越往北数值越大。
- 房龄中值:街区内的房龄中值,数值越小说明房屋越新。
- 房间总数:街区内的房间总数。
- 卧室总数:街区内的卧室总数。
- 人口数:街区内的居住总人数。
- 家庭数:街区内的家庭总数。
- 收入中值:街区内家庭的收入中值(以万美元计)。
To build a model, you extract the features that most contribute to the prediction. In order to make some of the features more relevant for predicting the median house value, instead of using totals we’ll calculate and use these ratios: rooms per house=total rooms/households, people per house=population/households, and bedrooms per rooms=卧室总数/房间总数。
在这种情况下,我们对以下标签和特征使用随机森林回归:
- 标签 → 房价中值
- 特征 → {"median age", "median income", "rooms per house", "population per house", "bedrooms per room", "longitude", "latitude" }
将文件中的数据加载到 DataFrame

第一步是将数据加载到 DataFrame。在以下代码中,我们指定了要加载到数据集的数据源和模式。
import org.apache.spark._
import org.apache.spark.ml._
import org.apache.spark.ml.feature._
import org.apache.spark.ml.regression._
import org.apache.spark.ml.evaluation._
import org.apache.spark.ml.tuning._
import org.apache.spark.sql._
import org.apache.spark.sql.functions._
import org.apache.spark.sql.types._
import org.apache.spark.ml.Pipeline
val schema = StructType(Array(
StructField("longitude", FloatType,true),
StructField("latitude", FloatType, true),
StructField("medage", FloatType, true),
StructField("totalrooms", FloatType, true),
StructField("totalbdrms", FloatType, true),
StructField("population", FloatType, true),
StructField("houshlds", FloatType, true),
StructField("medincome", FloatType, true),
StructField("medhvalue", FloatType, true)
))
var file ="/path/cal_housing.csv"
var df = spark.read.format("csv").option("inferSchema", "false").schema(schema).load(file)
df.show
result:
+---------+--------+------+----------+----------+----------+--------+---------+---------+
|longitude|latitude|medage|totalrooms|totalbdrms|population|houshlds|medincome|medhvalue|
+---------+--------+------+----------+----------+----------+--------+---------+---------+
| -122.23| 37.88| 41.0| 880.0| 129.0| 322.0| 126.0| 8.3252| 452600.0|
| -122.22| 37.86| 21.0| 7099.0| 1106.0| 2401.0| 1138.0| 8.3014| 358500.0|
| -122.24| 37.85| 52.0| 1467.0| 190.0| 496.0| 177.0| 7.2574| 352100.0|
+---------+--------+------+----------+----------+----------+--------+---------+---------+
In the following code example, we use the DataFrame withColumn() transformation, to add columns for the ratio features: rooms per house=total rooms/households, people per house=population/households, and bedrooms per rooms=卧室总数/房间总数。然后,我们缓存 DataFrame 并创建临时视图,以增强性能,同时提高 SQL 的易用性。
// 为特征创建比率
df = df.withColumn("roomsPhouse", col("totalrooms")/col("houshlds"))
df = df.withColumn("popPhouse", col("population")/col("houshlds"))
df = df.withColumn("bedrmsPRoom", col("totalbdrms")/col("totalrooms"))
df=df.drop("totalrooms","houshlds", "population" , "totalbdrms")
df.cache
df.createOrReplaceTempView("house")
spark.catalog.cacheTable("house")
汇总统计
Spark DataFrame 包含一些用于统计处理的内置函数。describe() 函数对数字列执行汇总统计计算,并将统计值作为 DataFrame 返回。以下代码显示了标签和某些特征的若干统计信息。
df.describe("medincome","medhvalue","roomsPhouse","popPhouse").show
result:
+-------+------------------+------------------+------------------+------------------+
|summary| medincome| medhvalue| roomsPhouse| popPhouse|
+-------+------------------+------------------+------------------+------------------+
| count| 20640| 20640| 20640| 20640|
| mean|3.8706710030346416|206855.81690891474| 5.428999742190365| 3.070655159436382|
| stddev|1.8998217183639696|115395.61587441359|2.4741731394243205| 10.38604956221361|
| min| 0.4999| 14999.0|0.8461538461538461|0.6923076923076923|
| max| 15.0001| 500001.0| 141.9090909090909|1243.3333333333333|
+-------+------------------+------------------+------------------+------------------+
DataFrame Corr() 函数用于计算 DataFrame 中两列数据的皮尔逊相关系数。此函数基于协方差法衡量两个变量之间的统计关系。相关系数值的范围为 1 到 -1,其中 1 表示完全正相关,-1 表示完全负相关,0 表示不相关。如下所示,收入中值和房价中值之间存在正相关关系。
df.select(corr("medhvalue","medincome")).show()
+--------------------------+
|corr(medhvalue, medincome)|
+--------------------------+
| 0.688075207464692|
+--------------------------+
以下散点图中,Y 轴表示房价中值,X 轴表示收入中值,此图表明二者之间为线性相关。

以下代码使用 DataFrame randomSplit 方法将数据集随机分为两部分,其中 80% 用于训练,20% 用于测试。
val Array(trainingData, testData) = df.randomSplit(Array(0.8, 0.2), 1234)
特征提取和流程
下列代码将创建 VectorAssembler(一种转换器),此转换器可用于流程中,将一组给定列组合为单个特征向量列。
val featureCols = Array("medage", "medincome", "roomsPhouse", "popPhouse", "bedrmsPRoom", "longitude", "latitude")
//将特征放入特征矢量列中
val assembler = new
VectorAssembler().setInputCols(featureCols).setOutputCol("rawfeatures")
以下代码将创建 StandardScaler(一种转换器),此转换器可用于流程中,通过使用 DataFrame 列汇总统计将特征扩展到单位方差,进而将特征标准化。
val scaler = new
StandardScaler().setInputCol("rawfeatures").setOutputCol("features").setWithStd(true.setWithMean(true)
在流程中运行这些转换器的结果是将向数据集中添加一个扩展的特征列,如下图所示。

流程中的最后一个元素是 RandomForestRegressor(一种估测器),此估测器通过特征向量和标签进行训练,然后返回 RandomForestRegressorModel(一种转换器)。
val rf = new
RandomForestRegressor().setLabelCol("medhvalue").setFeaturesCol("features")
在以下示例中,我们将 VectorAssembler、Scaler 和 RandomForestRegressor 置于一个流程中。流程将多个转换器和估测器相链接,以指定用于训练和使用模型的 ML 工作流程。
val steps = Array(assembler, scaler, rf)
val pipeline = new Pipeline().setStages(steps)

训练模型
Spark ML 支持通过一项名为“K 折交叉验证”的技术来测试不同的参数组合,从而确定 ML 算法的哪些参数值可生成最佳模型。通过 K 折交叉验证,数据将随机分为 K 个分区。每个分区都将作为测试数据集使用一次,其余分区则用于训练。然后,通过训练集生成模型,通过测试集评估模型,最终生成 K 模型准确性测量值。使准确性测量值达到最高的模型参数将生成最佳模型。

Spark ML 通过转换或估测流程支持 K 折交叉验证,此流程可使用名为“网格搜索”的过程来测试不同的参数组合,您可以在交叉验证工作流程中设置参数供其测试。

以下代码使用 ParamGridBuilder 构造用于模型训练的参数网格。我们会定义 RegressionEvaluator,其通过对比测试 medhvalue 列与测试预测列,对模型进行评估。我们使用 CrossValidator 来选择模型。CrossValidator 使用流程、参数网格和评估器来拟合训练数据集,并返回最佳模型。CrossValidator 使用 ParamGridBuilder 来迭代 RandomForestRegressor 估测器的 maxDepth、maxBins 和 numbTrees 参数,并评估模型,为得到可靠的结果,每个参数值重复三次。
val paramGrid = new ParamGridBuilder()
.addGrid(rf.maxBins, Array(100, 200))
.addGrid(rf.maxDepth, Array(2, 7, 10))
.addGrid(rf.numTrees, Array(5, 20))
.build()
val evaluator = new RegressionEvaluator()
.setLabelCol("medhvalue")
.setPredictionCol("prediction")
.setMetricName("rmse")
val crossvalidator = new CrossValidator()
.setEstimator(pipeline)
.setEvaluator(evaluator)
.setEstimatorParamMaps(paramGrid)
.setNumFolds(3)
// 拟合训练数据集并返回模型
val pipelineModel = crossvalidator.fit(trainingData)
接下来,我们可获得最佳模型,从而理清特征重要程度。结果表明,收入中值、每个房屋的人口数和经度是最重要的特征。
val featureImportances = pipelineModel
.bestModel.asInstanceOf[PipelineModel]
.stages(2)
.asInstanceOf[RandomForestRegressionModel]
.featureImportances
assembler.getInputCols
.zip(featureImportances.toArray)
.sortBy(-_._2)
.foreach { case (feat, imp) =>
println(s"feature: $feat, importance: $imp") }
result:
feature: medincome, importance: 0.4531355014139285
feature: popPhouse, importance: 0.12807843645878508
feature: longitude, importance: 0.10501162983981065
feature: latitude, importance: 0.1044621179898163
feature: bedrmsPRoom, importance: 0.09720295935509805
feature: roomsPhouse, importance: 0.058427239343697555
feature: medage, importance: 0.05368211559886386
在以下示例中,我们利用交叉验证过程获得了可生成最佳随机森林模型的参数,即此过程的返回值:最大深度为 2,最大箱数为 50,且棵树为 5。
val bestEstimatorParamMap = pipelineModel
.getEstimatorParamMaps
.zip(pipelineModel.avgMetrics)
.maxBy(_._2)
._1
println(s"Best params:\n$bestEstimatorParamMap")
result:
rfr_maxBins: 50,
rfr_maxDepth: 2,
rfr_-numTrees: 5
预测和模型评估
接下来,我们使用测试 DataFrame 来测量模型的准确性,测试 DataFrame 是从原始 DataFrame 随机分割的数据,占原始 DataFrame 的 20%,且未用于训练。
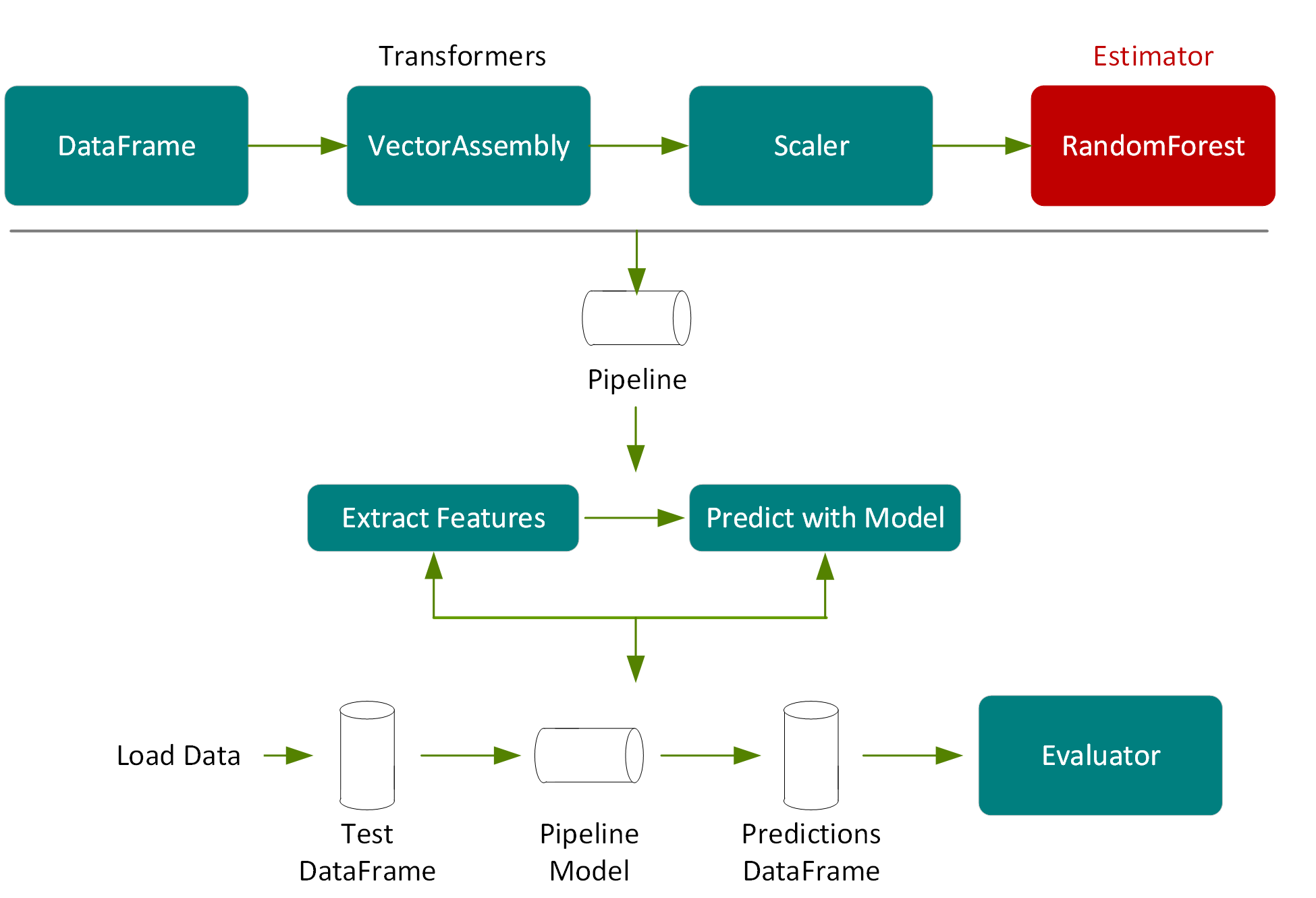
在以下代码中,我们在流程模型上调用转换,此操作将依照流程步骤将测试 DataFrame 传入特征提取阶段,通过由模型调整选出的随机森林模型进行估测,然后将预测结果返回到新的 DataFrame 列。
val predictions = pipelineModel.transform(testData)
predictions.select("prediction", "medhvalue").show(5)
result:
+------------------+---------+
| prediction|medhvalue|
+------------------+---------+
|104349.59677450571| 94600.0|
| 77530.43231856065| 85800.0|
|111369.71756877871| 90100.0|
| 97351.87386020401| 82800.0|
+------------------+---------+
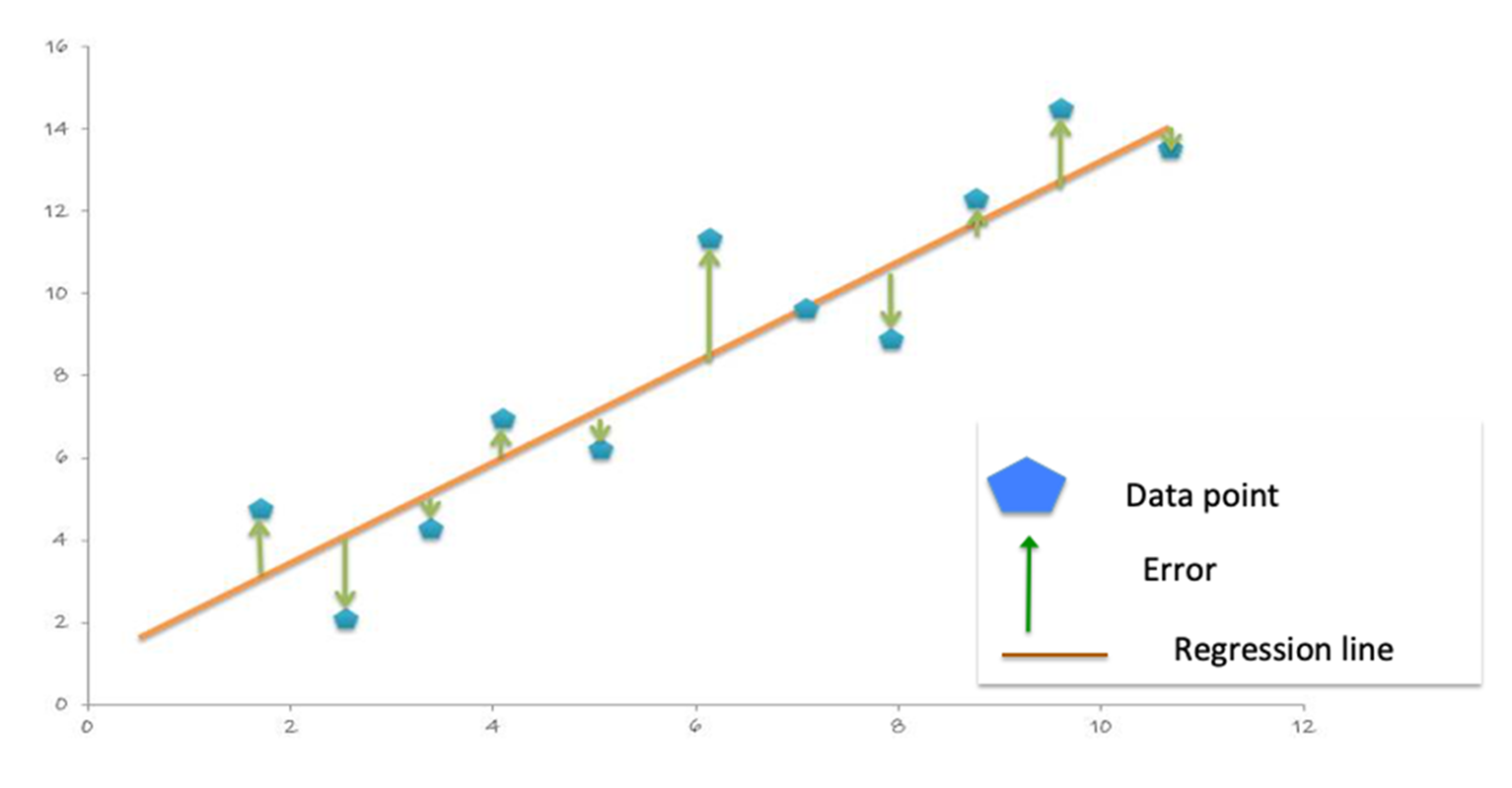
With the predictions and labels from the test data, we can now evaluate the model. To evaluate the linear regression model, you measure how close the predictions values are to the label values. The error in a prediction, shown by the green lines below, is the difference between the prediction (the regression line Y value) and the actual Y value, or label. (Error = prediction-label)。
平均绝对误差 (MAE) 是标签值与模型预测值之间的平均绝对差值。绝对值会消除所有负号。
MAE = sum(absolute(prediction-label)) / 观察次数)。
The Mean Square Error (MSE) is the sum of the squared errors divided by the number of observations. The squaring removes any negative signs and also gives more weight to larger differences. (MSE = sum(squared(prediction-label)) / 观察次数)。
均方根误差 (RMSE) 是 MSE 的平方根。RMSE 是预测误差的标准偏差。误差表示的是标签数据点距回归线的距离,而 RMSE 则表示误差的分散程度。
The following code example uses the DataFrame withColumn transformation, to add a column for the error in prediction: error=prediction-medhvalue。然后,我们显示预测值、房价中值和误差的汇总统计信息(以千美元计)。
predictions = predictions.withColumn("error",
col("prediction")-col("medhvalue"))
predictions.select("prediction", "medhvalue", "error").show
result:
+------------------+---------+-------------------+
| prediction|medhvalue| error|
+------------------+---------+-------------------+
| 104349.5967745057| 94600.0| 9749.596774505713|
| 77530.4323185606| 85800.0| -8269.567681439352|
| 101253.3225967887| 103600.0| -2346.677403211302|
+------------------+---------+-------------------+
predictions.describe("prediction", "medhvalue", "error").show
result:
+-------+-----------------+------------------+------------------+
|summary| prediction| medhvalue| error|
+-------+-----------------+------------------+------------------+
| count| 4161| 4161| 4161|
| mean|206307.4865123929|205547.72650805095| 759.7600043416329|
| stddev|97133.45817381598|114708.03790345002| 52725.56329678355|
| min|56471.09903814694| 26900.0|-339450.5381565819|
| max|499238.1371374392| 500001.0|293793.71945819416|
+-------+-----------------+------------------+------------------+
以下代码示例使用 Spark RegressionEvaluator,计算预测 DataFrame 的 MAE,并返回 36636.35(千美元)。
val maevaluator = new RegressionEvaluator()
.setLabelCol("medhvalue")
.setMetricName("mae")
val mae = maevaluator.evaluate(predictions)
result:
mae: Double = 36636.35
以下代码示例使用 Spark RegressionEvaluator,计算预测 DataFrame 的 RMSE,并返回 52724.70。
val evaluator = new RegressionEvaluator()
.setLabelCol("medhvalue")
.setMetricName("rmse")
val rmse = evaluator.evaluate(predictions)
result:
rmse: Double = 52724.70

保存模型
现在,我们可以将拟合的流程模型保存到分布式文件存储中,供以后在生产中使用。此操作可同时保存特征提取阶段和模型调整所选择的随机森林模型。
pipelineModel.write.overwrite().save(modeldir)
保存流程模型会得到一个元数据的 JSON 文件和一个模型数据的 Parquet。我们可以使用加载命令重新加载模型,原始模型和重新加载的模型相同:
val sameModel = CrossValidatorModel.load(“modeldir")
总结
本章中,我们讨论了回归、决策树和随机森林算法,介绍了 Spark ML 流程的基础知识,并通过实际示例来预测房价中值。
